\(\def\bra#1{\mathinner{\langle{#1}|}}\def\ket#1{\mathinner{|{#1}\rangle}}\def\braket#1{\mathinner{\langle{#1}\rangle}}\def\Bra#1{\left\langle#1\right|}\def\Ket#1{\left|#1\right\rangle}\)

5章 量子算術演算と量子論理演算

5.1

  • 復習
    • CCNOT = Toffoli gate
    • qubit はコピーできない
    • READ 以外の基本的な QPU 演算は可逆 (WRITE は READ + NOT でできる -> 2.3.4)
    • 演算が可逆なのはユニタリだから？

5.2

  • 量子ニブル (qunible) を使った算術演算を考える

5.2.1

5.3

  • 「複製不可能性に違反する」の説明は「可逆性の要件に違反する」の偽の命題を仮定していておかしい？ 演算がユニタリであることから可逆的であることが言えて、複製不可能性はそこから導かれるという方が自然？
  • +演算子は可逆性と複製不可能性に反するので += 演算子を実装する
    https://oreilly-qc.github.io/?p=5-2
  • QCEngine で add が実装されているのはこのあたり -> QCEngine/qcengine_int.js at master · machinelevel/QCEngine

5.4

5.5

  • 乗算は可逆にするのが困難
  • 可逆な演算の例: 二乗してから足す https://oreilly-qc.github.io/?p=5-3
  • b <- b*b は不可逆だが、 a += b*b の逆演算は a -= b*b で、可逆
  • 図5-10 は、以下のように理解できる。
    \(b = b_1 + 2b_2\) とおくと (\(b\)を2進数で表したときの1桁目を\(b_1\)、2桁目を\(b_2\))、
    \[ b^2 = {b_1}^2 + 4{b_1}{b_2} + 4{b_2}^2 \\ = {b_1} + 4{b_1}{b_2} + 4{b_2} \]
    (0と1は2乗しても変わらないため、\({b_1}^2 = b_1, {b_2}^2 = b_2 \) )
    図5-10の最初の４つの演算は \(+=b_1\) を表す。次の4つは \(+=2b_1b_2\) を2回やっている (\(b_1b_2\)は\(b_1, b_2\)がそれぞれ0または1であることから\(b_1~\text{AND} b_2~\)と同じ)。最後の2つが\(+=4b_2\)に対応。

(ここまで 2021/07/3)

5.6

5.6.1

5.6.2

  • https://oreilly-qc.github.io/?p=5-5
  • 位相に情報をエンコードするのに CPHASE や CZ を使っている
  • 書籍中の JavaScript 中の b.not(~1) のような部分が一見分かりにくい。まず ~1 は、1のビット演算の NOT、 つまり 32bit だったら一番下だけ0で、それ以外の31桁すべてが1になっている数を表す。なので、b.not(~1) は b.not(1...10) のようなイメージ。つまりレジスタ b に対して QPU の NOT 演算を、1つ目の qubit 以外全てに適用するという操作。
    今の場合、bは二桁しかないので、~1 は 10 と等価。

5.7

  • abs の実装例はないようなので自分たちでやってみた。

    • -1 (0b111) にabsを適用する場合。

      // Initialize
var num_qubits = 4;
qc.reset(num_qubits);
var a = qint.new(3, 'a');
var b = qint.new(1, 'b');
// prepare
qc.label('prepare');
a.write(0b111);
b.write(0b0);

qc.nop();

qc.label('XOR = CNOT');
qc.nop();
qc.nop();
qc.cnot(0x8, 0x4);
qc.nop();
qc.nop();

qc.label('2の補数');
qc.cnot(0x1|0x2|0x4, 0x8);
qc.cnot(0x4, 0x1|0x2|0x8);
qc.cnot(0x2, 0x1|0x8);
qc.cnot(0x1, 0x8);

      初期状態が \(\ket{a = -1 = \textrm{0b111},~b=0=\textrm{0b0}} = \ket{0111} = \ket{7} \) で、終状態が \(\ket{a = 1 = \textrm{0b001},~b=1=\textrm{0b1}} = \ket{1001} = \ket{9} \) となっている。

      abs(-1)

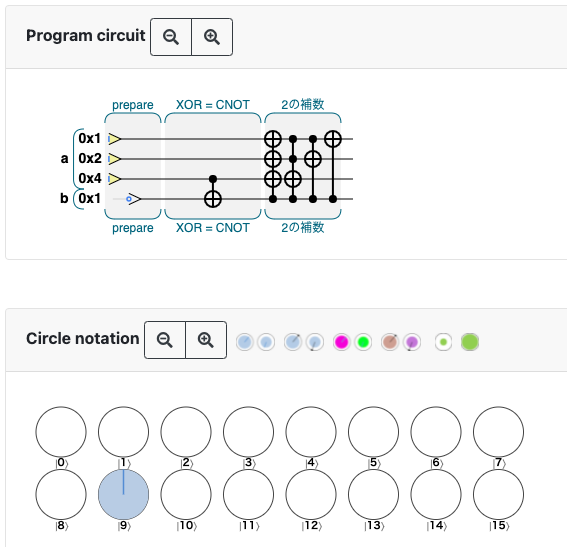
    • 1と-1の重ね合わせにabsを適用する場合。

      var num_qubits = 4;
qc.reset(num_qubits);
var a = qint.new(3, 'a');
var b = qint.new(1, 'b');
// prepare
qc.label('prepare');
a.write(0);
b.write(0);
qc.nop();
qc.label('｜0〉+｜2〉');
qc.nop();
qc.had(0x2);
qc.nop();
qc.label('subtract(1)');
a.subtract(1);
qc.nop();

qc.label('abs');

qc.cnot(0x8, 0x4);

qc.cnot(0x1|0x2|0x4, 0x8);
qc.cnot(0x4, 0x1|0x2|0x8);
qc.cnot(0x2, 0x1|0x8);
qc.cnot(0x1, 0x8);

      はじめに \(\ket{0}\) と \(\ket{2}\) の重ね合わせを作ってから \(-1\) すると \(\ket{-1} = \ket{7}\) と \(\ket{1}\) の重ね合わせになる。これに abs を適用すると \(\ket{1}=\ket{0001}\) と \(\ket{9}=\ket{1001}\) の重ね合わせになる。このとき、 \(a\) に対応する部分はどちらの状態でも \(001\) で、絶対値は等しい。 (-1と1の重ね合わせを作る方法を思いついたふぇるみうむ氏かしこい！)

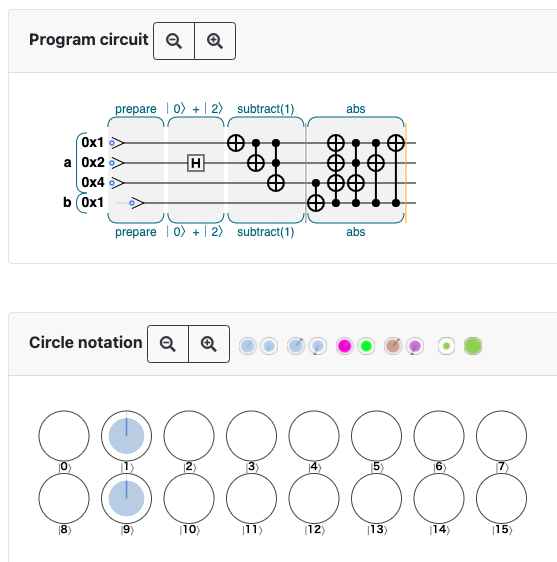
      abs(-1, 1)

(ここまで 2021/07/25)

5.8

  • スクラッチキュビットは演算を可逆にするために導入したが、もつれやすい
  • もつれを戻すために演算を巻き戻すことをアンコンピュートと呼ぶ
  • アンコンピュートする前に値を足したり XOR (CNOT) したり、位相情報に変換するなどして計算結果を保存する

5.9

  • NAND ゲートがあると、 AND, OR, NOT, XOR などが作れる
  • CNOT ゲート (トフォリゲート) で NAND と同じものを作れる https://oreilly-qc.github.io/?p=5-6
  • 他にも NOT, AND, NAND, XOR, OR, NOR を作ったものが図5-25

5.10

この章では重ね合わせ状態で計算する方法を見て来たが、次の章では結果を読み出す方法 (振幅増幅) を見て行く。